E3: Architecting Intelligence - Deep Learning

Architecture and Artificial Intelligence through Deep Learning

Introduction

In the previous episode, I explored the core principles of Machine Learning. Now, I transition to Deep Learning (DL), focusing on Neural Networks, the foundational aspect of DL. Neural Networks are inspired by the human brain's structure, aiding the creation of advanced intelligent systems. This shift to DL represents a deeper exploration into machine intelligence, allowing for more complex data interpretations. As I go into Neural Networks, and later, CNNs and RNNs, let me set the stage for a detailed exploration of DL from an architectural standpoint.

The history of Deep Learning (DL) reflects a gradual evolution of understanding and technological advancements. Here's a concise list of key milestones and notable figures in the field:

1. Origins in Neural Networks: The concept of neural networks dates back to the 1940s. In 1943, Warren McCulloch and Walter Pitts proposed a computational model of an artificial neuron, laying the groundwork for future developments in neural network theories​¹​.

2. Perceptron Era: In 1958, Frank Rosenblatt introduced the Perceptron, a type of artificial neuron, which became a foundational element of neural network research.

3. Backpropagation Algorithm: In the 1980s, the backpropagation algorithm was introduced, which is crucial for training multi-layer neural networks. This algorithm significantly contributed to the development and training of deep neural networks.

4. Convolutional Neural Networks (CNNs): In 1998, Yann LeCun introduced LeNet-5, a pioneering convolutional neural network that significantly influenced the development of CNNs.

5. Deep Learning Renaissance: With the advent of big data and increased computational power, the early 2000s saw a resurgence in interest and advancements in deep learning. Pioneers like Geoffrey Hinton, Yann LeCun, and Yoshua Bengio played pivotal roles during this period.

6. ImageNet Competition: The 2012 ImageNet competition marked a significant milestone with the introduction of AlexNet, a deep convolutional neural network that drastically reduced error rates in image recognition tasks, propelling DL to the forefront of AI research.

7. Recent Advancements: Recent years have witnessed a rapid proliferation of deep learning applications across various domains, powered by advancements in neural network architectures, training algorithms, and the availability of vast amounts of data.

Some of the main sources that I used to understand Deep Learning are

1. "Deep Learning" by Ian Goodfellow, Yoshua Bengio, and Aaron Courville.

2. “Deep Learning” by Yann LeCun, Yoshua Bengio & Geoffrey Hinton 

3. "Neural Networks and Deep Learning" by Michael Nielsen.

4. "Deep Learning: A Critical Appraisal" by Gary Marcus.

And some amazing Substack that facilitate my understandment with two specific post are

How to build Large AI Models like ChatGPT efficiently

Deep Learning Weekly: Issue #275

Neural Networks

In my journey into Deep Learning, the first stop is Neural Networks (NNs). Being a cornerstone for many Deep Learning applications, understanding NNs is crucial for an architect to leverage AI in their solutions.

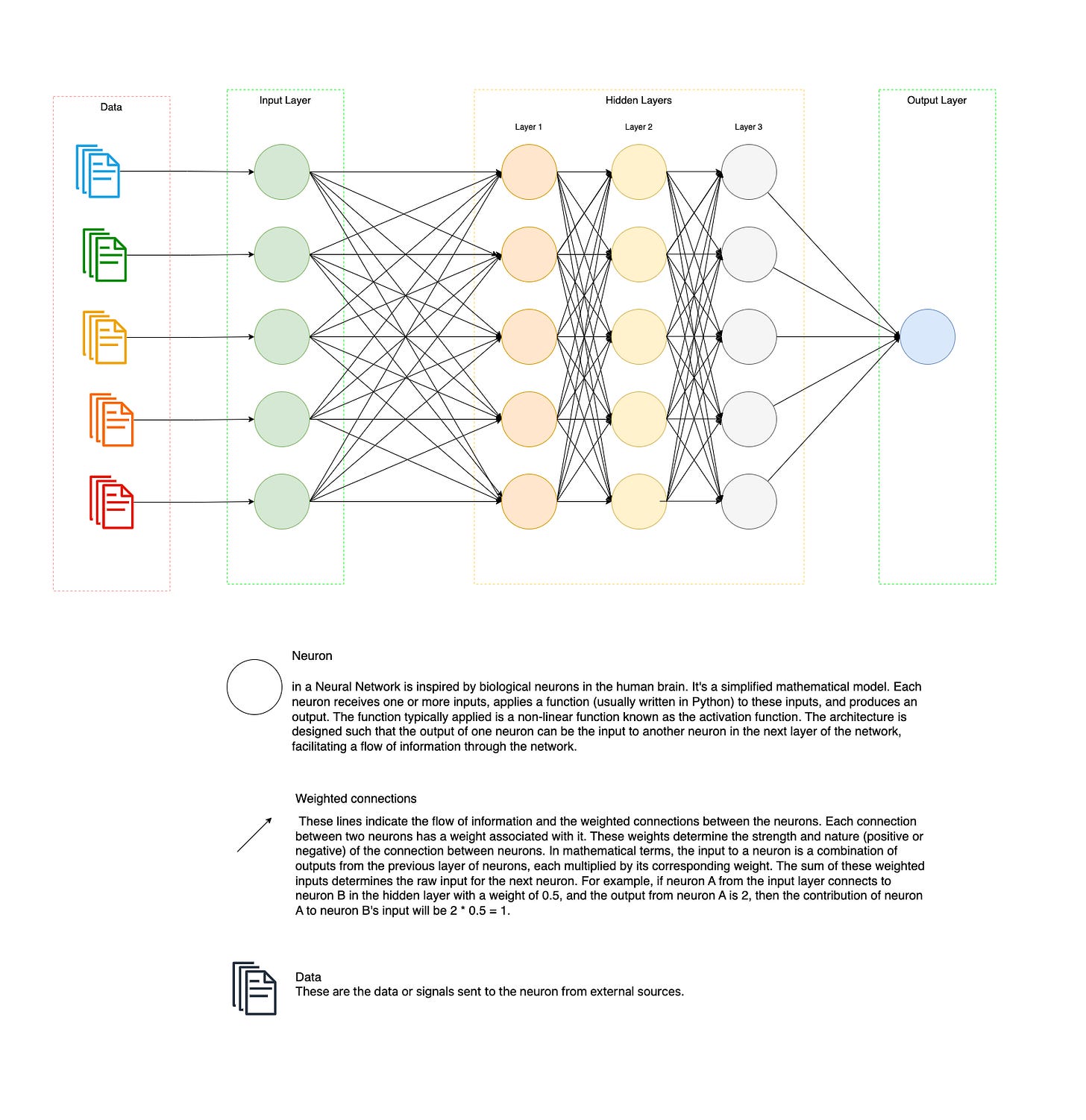
A Neural Network is a computational model inspired by the human brain's interconnected neuron structure. It's a framework for building and training models to understand and solve complex patterns, making them vital for various AI applications.

Components of NN

Input Layer

The initial layer where the model receives its data. Each neuron in this layer corresponds to one feature in the data set, acting as the entry point for data to flow into the network.

Hidden Layers

These are the layers between the input and output layers, where the “Magic” happens. Each neuron in a hidden layer receives inputs from all neurons in the previous layer, applies a transformation (typically non-linear), and passes its output to all neurons in the next layer. The presence of multiple hidden layers is what makes a Neural Network "deep" - leading to the term Deep Learning.

Output Layer

The final layer where the model makes its predictions. The number of neurons in this layer corresponds to the number of possible outputs.

The connections between neurons are represented by weights, which are adjusted during training to minimize the error between the model's predictions and the actual target values.

Check this diagram below that I have created to represent a NN

Here is a Python code example that translate the diagram above, using TensorFlow

# neural_network.py

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

# Based on the diagram provided:
# - Input Layer: 4 neurons (Green Circles)
# - Hidden Layer 1: 6 neurons (First set of Orange Circles)
# - Hidden Layer 2: 3 neurons (Second set of Orange Circles)
# - Hidden Layer 3: 3 neurons (Grey Circles)
# - Output Layer: 1 neuron (Blue Circle)

# 1. Initializing the Sequential Model
model = keras.Sequential()

# 2. Adding the Input Layer
# Corresponding to the 4 Green Circles in the diagram.
# Each neuron corresponds to a distinct feature of the input

model.add(layers.Dense(units=4, activation='relu', input_dim=4, name="input_layer"))

# 3. Adding Hidden Layers

# First Hidden Layer - corresponds to the 6 Orange Circles in the diagram.
# Neurons in hidden layers process the incoming data from the previous layer and transform it using an activation function.

model.add(layers.Dense(units=6, activation='relu', name="hidden_layer_1"))

# Second Hidden Layer - corresponds to the 3 Orange Circles in the diagram.

model.add(layers.Dense(units=3, activation='relu', name="hidden_layer_2"))

# Third Hidden Layer - corresponds to the 3 Grey Circles in the diagram.

model.add(layers.Dense(units=3, activation='relu', name="hidden_layer_3"))

# 4. Adding the Output Layer
# Corresponding to the single Blue Circle in the diagram.
# The neuron in the output layer produces the final prediction of the model.

model.add(layers.Dense(units=1, name="output_layer"))

# 5. Compile the model
# 'mean_squared_error' is a common loss function for regression problems.
# The optimizer 'adam' is an algorithm that adjusts neuron weights to minimize the error during training.

model.compile(optimizer='adam', loss='mean_squared_error')

# NOTE on Nodes (Neurons):
# - Nodes in the input layer represent distinct features of the input data.
# - Nodes in hidden layers process the data, applying transformations using their weights and activation functions.
# - The node in the output layer provides the final prediction of the neural network.
# 
# NOTE on Weights:
# Every connection between the neurons in the diagram has a corresponding weight in the model.
# These weights determine how much influence one neuron has on the next neuron it's connected to.
# During training, the model adjusts these weights to better fit the training data and reduce prediction errors.

It’s important to understand that each node in the diagram computes a weighted sum of its inputs and then applies an activation function to this sum. To be specific the activation sum is mathematical function that determines the output of a neuron.

In the context of the code I provided, I’m using the activation functions that TensorFlow provides. Specifically, I’ve chosen the relu (Rectified Linear Unit) activation function for the input and hidden layers.

model.add(layers.Dense(units=6, activation='relu', name="hidden_layer_1"))

relu Activation Function: The Rectified Linear Unit (ReLU) is one of the most widely used activation functions in deep neural networks, especially for feedforward and convolutional neural networks. Mathematically, it's defined as

\(f(x)=max(0,x)\)

The function returns x if x is greater than or equal to 0, and returns 0 otherwise. The ReLU function is non-linear, which means it allows for complex mappings and is computationally efficient, making the network easier and faster to train.

The activation='relu' argument specifies that the relu activation function should be used for the neurons in that layer.

TensorFlow provides a variety of other activation functions like sigmoid, tanh, softmax, and more. The choice of activation function depends on the specific task, the nature of the data, and the architecture of the neural network. In many cases, ReLU (or its variants like LeakyReLU or ParametricReLU) is a good default choice for hidden layers in feedforward neural networks. Potential If you have a specific reason or hypothesis, you can customize and create a neural network where each neuron or a group of neurons performs a different specific operation,

Deep Learning, via Neural Networks, has significantly expanded the capabilities of machine learning, addressing complex problems that were previously unsolvable with traditional machine learning models.

Neural Networks vs Classic Machine Learning:

Neural Networks, forming the core of Deep Learning, have a number of advantages over traditional machine learning methods:

1. Automatic Feature Extraction: Neural Networks have the capability to automatically discover and learn features from raw data. This is a significant advantage over traditional machine learning methods where feature engineering is manual, and domain expertise is required to design features.

2. Complex Problem-Solving: They can model complex, non-linear relationships, which is crucial for solving complex problems that traditional machine learning models struggle with.

3. Scalability: Neural Networks tend to perform better as the size of the data increases, making them highly scalable.

4. Multi-dimensional and Sequential Data Handling: They are adept at handling multi-dimensional and sequential data, which is invaluable in fields like image and video recognition, and natural language processing.

One of the part that fascinate me the most is the Automatic Feature Engineering

Feature engineering or feature extraction or feature discovery is the process of extracting features (characteristics, properties, attributes) from raw data.¹

For instance, in a dataset related real estate prices, features might include the size of the property, the number of rooms, the neighborhood's crime rate, proximity to schools, etc. In a text classification problem, features might include word counts, the frequency of certain words, the length of the text, etc.

In traditional ML, much of the feature engineering needs to be done manually which can be time-consuming and require domain expertise. On the other hand, deep learning models, especially neural networks, are capable of automatic feature extraction from raw data. This is one of the reasons why deep learning models have gained popularity for complex tasks such as image and text analysis where manual feature engineering would be incredibly challenging or impractical.

Convolutional Neural Networks (CNN)

Convolutional Neural Networks (CNN) are a class of deep learning models specially designed to process grid-like data, such as images. Unlike traditional Neural Networks, CNNs have a unique architecture well-suited to automatically and adaptively learn spatial hierarchies of features from input data.

Components of CNN

Convolutional Layer

This is the core building block of a CNN. The layer's parameters consist of a set of learnable filters (or kernels), which have a small receptive field, but extend through the full depth of the input volume. During the forward pass, each filter is convolved across the width and height of the input volume, computing the dot product between the entries of the filter and the input, producing a 2-dimensional activation map.

Pooling Layer

Pooling (subsampling or down-sampling) reduces the dimensionality of each feature map and retains the most essential information. It could be done through various methods like max pooling, average pooling, etc.

Fully Connected Layer

Fully connected layers connect every neuron in one layer to every neuron in the next layer, which is the same as traditional neural networks as explained above.

Activation Functions

Activation functions like ReLU (Rectified Linear Unit) introduce non-linear properties to the system. Their main purpose is to convert a input signal of a node in a A-NN to an output signal. That output signal now is used as a input in the next layer in the stack.

Output Layer

The final layer which produces the output based on the learned features

Now I used TensorFlow's Keras API to create a Convolutional Neural Network (CNN) model that matches the diagram.

# CNN_Model.py

import tensorflow as tf
from tensorflow.keras import layers, models

# Initializing the CNN model
model = models.Sequential()

# Referencing the Image Icon in the provided diagram
# Assuming the input image has a shape of (64, 64, 3), which is a standard for RGB images.

# Convolution Block 1 (referenced as Blue in the diagram)
model.add(layers.Conv2D(32, (3,3), activation='relu', input_shape=(64, 64, 3)))
model.add(layers.MaxPooling2D((2, 2)))

# Convolution Block 2 (referenced as Green in the diagram)
model.add(layers.Conv2D(64, (3,3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))

# Convolution Block 3 (referenced as Orange in the diagram)
model.add(layers.Conv2D(128, (3,3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))

# Flatten Layer (referenced as Gray in the diagram)
model.add(layers.Flatten()) 

# Fully Connected Layer 1 (represented as circles in "Layer 1")
model.add(layers.Dense(128, activation='relu'))

# Fully Connected Layer 2 (represented as circles in "Layer 2")
model.add(layers.Dense(64, activation='relu'))

# Fully Connected Layer 3 (represented as circles in "Layer 3")
model.add(layers.Dense(32, activation='relu'))

# Output Layer (represented as the "Output" Yellow rectangle in the diagram)
# Assuming a binary classification task for simplicity

model.add(layers.Dense(1, activation='sigmoid')) # Use 'softmax' for multi-class problems.

model.compile(optimizer='adam',
              loss='binary_crossentropy', # Use 'categorical_crossentropy' for multi-class problems.
              metrics=['accuracy'])

# Printing the model summary for clarity
model.summary()

1. I start by importing the necessary modules from TensorFlow's Keras API.

2. The Sequential model is initialized, indicating that layers are added in sequence.

3. Following the structure of the provided image:

   • We add three Conv2D layers for convolution operations, where each layer attempts to identify patterns in the image. They are followed by MaxPooling2D layers which down-sample the spatial dimensions of the previous layer.

   • The Flatten layer converts the 2D matrices from previous layers into a 1D vector.

   • Three fully connected Dense layers follow the flattening operation. They perform high-level reasoning based on the patterns identified in previous layers.

   • Finally, an output Dense layer is added. I assumed a binary classification task, but this can be modified based on the number of classes in the task.

4. The compile method prepares the model for training, specifying the optimizer, loss function, and evaluation metric.

5. model.summary() method prints a summary of the model's architecture, so you can visually inspect the sequence of layers.

As an architect, CNNs opens up a new spectrum of design solutions. With CNNs, applications like real-time image and video recognition, or even complex anomaly detection in multidimensional data become feasible. The automated feature extraction capability of CNNs can significantly reduce the time and effort required in the data preprocessing stage, allowing for quicker deployments and iterations. Understanding the architectural underpinnings and the potential of CNNs can lead to more informed decisions when designing systems revolving around image or video data processing.

Recurrent Neural Networks (RNN)

Recurrent Neural Networks (RNN)² are a class of artificial neural networks where connections between nodes form a directed graph along a temporal sequence. Unlike traditional neural networks, RNNs have a "memory" that captures information about what has been calculated so far. This feature makes RNNs extremely useful for tasks involving sequential data like time series prediction, natural language processing, and speech recognition.

Components of RNN

Recurrent Layer

The recurrent layer consists of a loop that connects the current time step to the previous time step, enabling the network to use information from the past in the current computation.

Hidden State

The hidden state captures information from previous time steps. It's like the memory of the network, retaining crucial insights from past data to help in current processing.

Output Layer

The output layer generates the final output for the current time step based on the current input and the hidden state.

Activation Functions

Similar to other neural networks, activation functions introduce non-linearity into the system, which enables the network to learn from the error, and make adjustments to the weights of the inputs.

Loss Function

The loss function (like Cross-Entropy or Mean Squared Error) measures the discrepancy between the predicted output and the true output, guiding the optimization of the network weights.

Recurrent Mechanism

Hidden State

The primary component responsible for memory in RNNs is the hidden state. The hidden state is a representation that captures information from past inputs and carries it forward to help process future inputs. At each time step, the hidden state is updated based on the current input and the previous hidden state. This way, it encapsulates information from all the previous steps up to the current step.

# Simplified RNN mechanism

hidden_state = initial_state

# This state will be updated over time
# Combine the input and the current state to generate the new state
# Now, hidden_state contains information from the past and the current input

for input in sequence: 
hidden_state = activation_function(W * input + U * hidden_state + b)  

Recurrent Connections

The recurrent connections are what allow the network to maintain this memory. They create a looped pathway that feeds the hidden state from one step back into the network for the next step. This recurrent loop essentially creates a form of memory, where information from previous steps can continue to influence the processing of new steps.

Memory in Action

Consider a simple task of predicting the next word in a sentence. If the current word is "sky", and the previous words were "The", and "blue", an RNN could use its memory of these previous words to help predict that the next word might be "is". The memory in this case helps the RNN understand the context in which the current word appears.

Memory Duration

The ability of RNNs to maintain this memory over many steps is both its strength and its weakness. While it's useful for understanding context over sequences, the memory in basic RNNs tends to be quite short-term due to the vanishing gradient problem, which makes it hard for the network to learn from interactions occurring over longer sequences. Advanced variants of RNNs like Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRUs) have been developed to address this, providing longer-term memory capabilities and making RNNs even more powerful for handling sequential data.

In summary, memory in RNNs facilitates the processing and understanding of sequential or temporal data by allowing the network to use information from past inputs while processing current inputs, which is crucial for tasks like language modeling, time series prediction, and many other applications where understanding context over time is essential.

I again used TensorFlow's Keras API to create a Recurrent Neural Network (RNN) model that matches the diagram.

# RNN_Model.py

import tensorflow as tf
from tensorflow.keras import layers, models

# Initializing the model

model = models.Sequential()

# Input Layer (represented as green circles in the diagram)
# Assuming input data is of shape (n, m) where n represents features and m represents samples.

model.add(layers.Input(shape=(None,)))

# Hidden Layer 1 (referenced as "Layer 1" in the diagram)
# Assuming 5 neurons based on the diagram

model.add(layers.Dense(5, activation='relu'))

# Recurrence within Hidden Layer (indicated by the dashed red line)
# A simple recurrence can be implemented using a SimpleRNN layer in Keras.
# Here, we're assuming recurrence in the second hidden layer.
# Assuming 5 neurons

model.add(layers.SimpleRNN(5, activation='relu', return_sequences=True)) 

# Hidden Layer 2 (referenced as "Layer 2" in the diagram)
# After the SimpleRNN layer, the data will be 3D (batch_size, timesteps, features).
# So, we need to flatten the data to feed into the Dense layer.

model.add(layers.Flatten())
model.add(layers.Dense(5, activation='relu')) # Assuming 5 neurons based on the diagram

# Output Layer (represented as the blue circle in the diagram)
# Assuming a single output for regression task.

model.add(layers.Dense(1))

# Compiling the model

model.compile(optimizer='adam', loss='mean_squared_error')

# Printing the model summary for clarity

model.summary()

1. The Sequential model is initialized.

2. The Input layer is added to define the input shape of the data. The actual shape would be dependent on the dataset.

3. The first hidden layer (Layer 1 in the diagram) is added with 5 neurons, as visually indicated.

4. To capture the recurrence shown in the diagram, a SimpleRNN layer is added. This layer can capture sequences in the data. The layer has 5 neurons, aligning with the number of circles in the diagram.

5. As the SimpleRNN produces 3D output data (batch_size, timesteps, features), we use the Flatten layer to reshape it for the next dense layer.

6. Another dense hidden layer (Layer 2 in the diagram) with 5 neurons follows.

7. The final output layer is added. For simplicity, I assumed this is a regression task with a single output. If it's a classification task, you might want to use an activation like sigmoid or softmax and adjust the loss function accordingly during compilation.

8. The model is compiled using the Adam optimizer and a mean squared error loss, typically used for regression tasks.

Understanding RNNs provides a way to design solutions around problems involving sequential data. The ability to handle temporal dynamics opens a new possibilities in application areas like real-time analytics, natural language processing, and many others. From an architectural standpoint, understanding the mechanisms of RNNs and their potential applications can be a cornerstone in building intelligent systems capable of interpreting and reacting to sequential or time-dependent data.

Conclusion

Deep Learning is a paradigm where machines can learn from data at a depth which was previously unthought of. As a software architect, understanding and leveraging the intricacies of Neural Networks, CNNs, and RNNs opens up a frontier of possibilities in designing intelligent systems capable of self-learning, recognizing complex patterns, and making informed decisions over time.

As this episode comes to a close, the anticipation for the subsequent explorations into the heart of AI keeps the quest for knowledge aflame. The journey continues to be as exhilarating as it is enlightening, each step forward is a step into the future of software architecture, where machines not only compute but learn, adapt, and evolve.

As we close the chapter on Neural Networks, our next episode will delve into Large Language Models (LLMs) and the transformative world of Generative AI.

Here's a brief on what to anticipate:

1. LLMs:

   • Exploring Transformer Architecture and Attention Mechanisms.

   • Strategies of Pre-training and Fine-tuning.

2. Natural Language Processing:

   • Insights into Text Mining and Sentiment Analysis.

3. Generative AI:

   • Unveiling Generative Adversarial Networks (GANs) and Text Generation Techniques.

Stay tuned for the next episode in this AI Odyssey.

1. https://en.wikipedia.org/wiki/Feature_engineering

2. https://developer.ibm.com/articles/cc-cognitive-recurrent-neural-networks/